Задача
Точки K, L, M и N на сторонах AB, BC, CD и DA квадрата ABCD образуют еще один квадрат. DK пересекает NM в точке E, а KC пересекает LM в точке F.
Докажите, что EF || AB.
Решение
Обозначим точки пересечения прямых MN и LM с прямой AB как P и Q соответственно. Треугольники AKN, BLK, CML и DMN равны по гипотенузе и острому углу. Пусть AK = a и BK = b, тогда BL = CM = DN = a, CL = MD = NA = b. Поскольку треугольники PKN и QLK – прямоугольные, PA·a = b² и BQ·b = a². Из подобия треугольников PEK и MED получим, что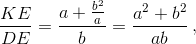 
а из подобия треугольников QFK и MFC следует, что 
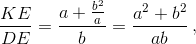Значит, KE : DE = FK : CF и EF || AB.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет