Задача
Окружности ω1 и ω2, касающиеся внешним образом в точке L, вписаны в угол BAC. Окружность ω1 касается луча AB в точке E, а окружность ω2 – луча AC в точке M. Прямая EL пересекает повторно окружность ω2 в точке Q. Докажите, что MQ || AL.
Решение
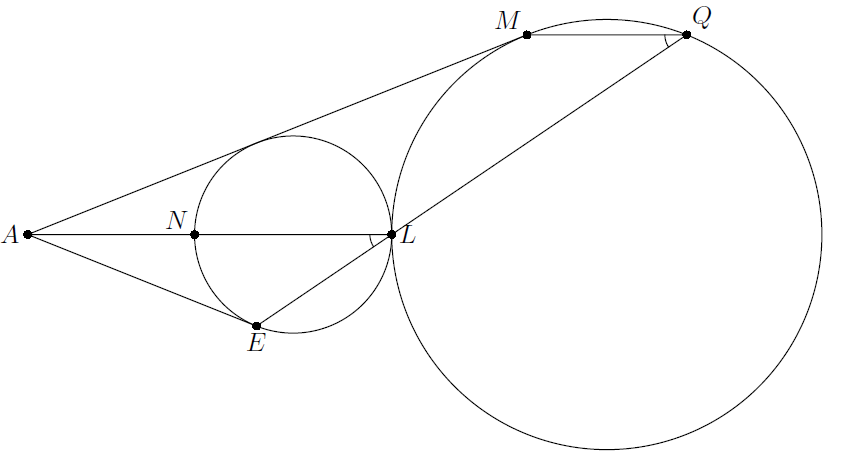
Пусть N – вторая точка пересечения ω1 с AL (см. рис.). Тогда композиция симметрии относительно AL и гомотетии с центром A переводит дугу NE в дугу LM. Следовательно, опирающиеся на эти дуги углы ALE и MQE равны, что равносильно утверждению задачи.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет