Задача
Дан прямоугольник ABCD. Через точку B провели две перпендикулярные прямые. Первая прямая пересекает сторону AD в точке K, а вторая продолжение стороны CD в точке L. Пусть F – точка пересечения KL и AC. Докажите, что BF ⊥ KL.
Решение
Решение 1:Так как ∠ABK = ∠CBL, треугольники ABK и CBL подобны. Значит, треугольники ABC и KBL также подобны и ∠BKF = ∠BAF. Следовательно, четырёхугольник ABFK – вписанный и ∠BFK = 90° (см. рис.).
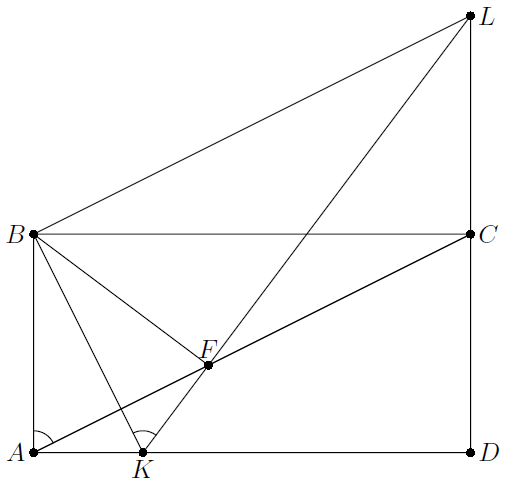
Решение 2:Заметим, что точка B лежит на описанной окружности треугольника KLD. Точки A и C являются основаниями перпендикуляров, опущенных из точки B на прямые KD и DL. А значит, основание перпендикуляра, опущенного из точки B на прямую KL, согласно задаче 152421 лежит на прямой Симсона AC, то есть совпадает с точкой F, что и требовалось доказать.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь