Задача
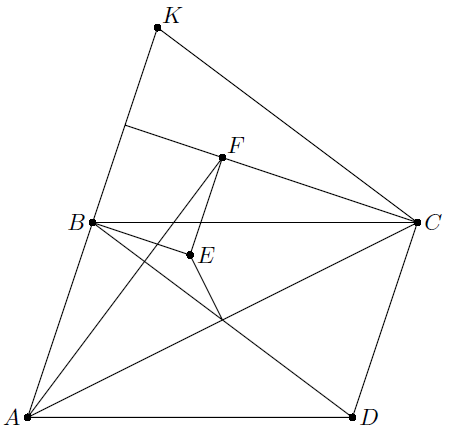
Перпендикуляр, восстановленный в вершинеCпараллелограммаABCDк прямойCD, пересекает в точкеFперпендикуляр, опущенный из вершиныAна диагональBD, а перпендикуляр, восстановленный из точкиBк прямойAB, пересекает в точкеEсерединный перпендикуляр к отрезкуAC. В каком отношении отрезокEFделится сторонойBC?
Решение
Пусть точка K симметрична A относительно B. Тогда E – центр описанной окружности треугольника ACK. С другой стороны, так как BKCD – параллелограмм, то AF ⊥ CK, то есть F – ортоцентр треугольника ACK (см. рис.). Следовательно, медиана CB делит EF в отношении 1 : 2 (см. задачу 155595).
Ответ
1 : 2.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет