Задача
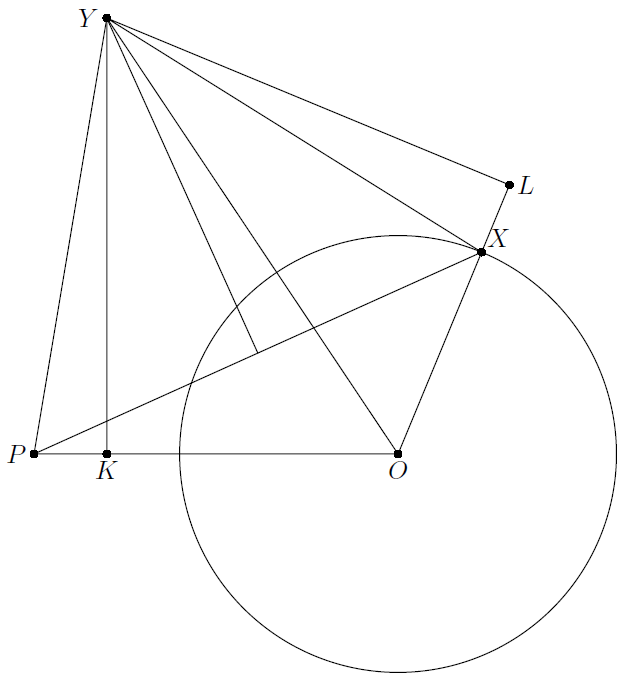
Дана окружность с центром O и не лежащая на ней точка P. Пусть X – произвольная точка окружности, Y – точка пересечения биссектрисы угла POX и серединного перпендикуляра к отрезку PX. Найдите геометрическое место точек Y.
Решение
Пусть K, L – проекции точки Y на OP и OX. Из определения точки Y следует, что YP = YX и YK = YL. Значит треугольники YKP и YLX равны, то есть
XL = PK. Кроме того, OL = OK. Поскольку длины отрезков OP и OX не равны, одна из них равна сумме длин отрезков OK и KP, а другая – их разности. Следовательно, OK = ½ (OP + OX) (см. рис.), то есть точка K фиксирована. Очевидно, что любая точка перпендикуляра, восстановленного из точки K к прямой OP, принадлежит искомому ГМТ.
Ответ
Прямая, перпендикулярная лучу OP и пересекающая его в точке, удалённой от O на расстояние ½ (OP + OX).
Чтобы оставлять комментарии, войдите или зарегистрируйтесь