Задача
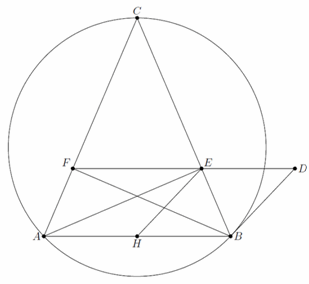
Вокруг равнобедренного треугольника ABC с основанием AB описана окружность и в точке B проведена касательная к ней. Из точки C проведён перпендикуляр CD к этой касательной, также проведены высоты AE и BF. Докажите, что точки D, E, F лежат на одной прямой.
Решение
Пусть CH – третья высота треугольника. Так как ∠CBD = ∠A = ∠B, треугольники CBD и CBH равны, то есть BD = BH. Кроме того, EH – медиана прямоугольного треугольника AEB, значит, EH = HB = BD и ∠BEH = ∠EBH = ∠EBD. Следовательно, EDBN – параллелограмм (см. рис.) и DE || AB. Поскольку и EF || AB, прямые DE и EF совпадают.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет