Задача
Дан прямоугольный треугольник ABC. На катете AB во внешнюю сторону построен равносторонний треугольник ADB, а на гипотенузе AC во внутреннюю сторону – равносторонний треугольник AEC. Прямые DE и AB пересекаются в точке M. Весь чертёж стерли, оставив только точки A и B. Восстановите точку M.
Решение
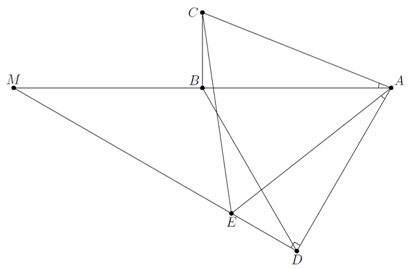
При повороте на 60° треугольник ABC переходит в треугольник ADE. Значит, эти треугольники равны и ∠ADE = 90°. Поэтому треугольник ADM – прямоугольный с углом A = 60°. Следовательно, AM = 2AD = 2AB (см. рис.), то есть точка M симметрична A относительно B.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет