Четырехугольник: доказательство параллельных сторон в олимпиадной зада

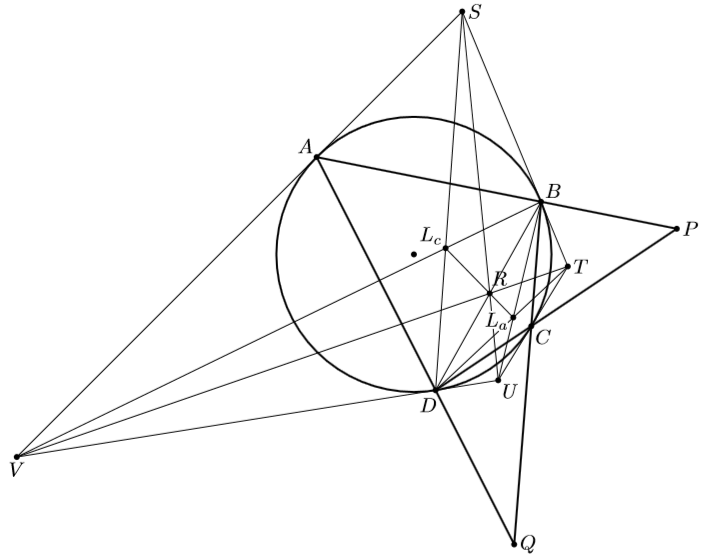
  Предположим, что четырёхугольник L_aL_bL_cL_d вписанный, но в четырёхугольнике ABCD нет параллельных сторон. Пусть прямые AB и CD пересекаются в точке P, AD и BC – в точке Q, а AC и BD – в точке R (см. рис.). Далее, пусть касательные к окружности в точках A, B, C и D образуют четырёхугольник STUV, как показано на рисунке; некоторые из точек S, T, U и V могут быть бесконечно удалёнными.

  Согласно задаче153121диагоналиSUиTVописанного четырёхугольникаSTUV пересекаются в точкеR. Заметим, что точкиL_a иL_c являютсяточками ЛемуанатреугольниковBCD иBAD соответственно (это следует из условия и задачи156978), поэтомуL_a– точка пересеченияBUиDT, аL_c– точка пересеченияBVиDS. Применивтеорему Паппа(см. задачу158435) к тройкам точек   {S, B, T}  и  {U, D, V},  получим, что точкаR лежит на прямойL_aL_c. АналогичноR лежит наL_bL_d.   Обозначим черезWточку пересеченияSTиUV, а черезX – точку пересеченияSVиUT(эти точки могут быть бесконечно удалёнными). Точно так же докажем, чтоL_aL_bиL_cL_dпересекаются в точкеP, аL_aL_dиL_bL_c– в точкеQ.   Так как вершины треугольникаPQR являются точками пересечения диагоналей и противоположных сторон четырёхугольникаABCD, вершины этого треугольника являютсяполюсамиего сторон относительно описанной окружности Ω четырёхугольникаABCD (такая окружность называетсяавтополярной окружностьютреугольникаPQR). По тем же причинам описанная окружность ω четырёхугольникаL_aL_bL_cL_d также является автополярной относительноPQR. Но для треугольника может существовать максимум одна автополярная окружность. Следовательно, Ω совпадает с ω, что невозможно, так как точкиL_a, L_b, L_c иL_d лежат внутри Ω.

Ответ задачи отсутствует