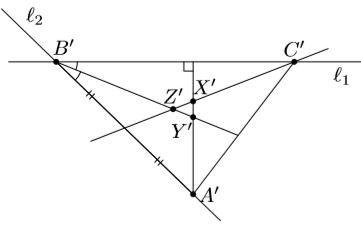
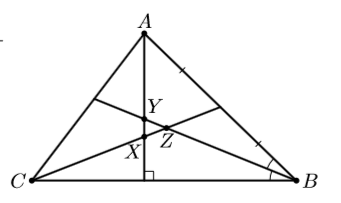
Пусть X, Y, Z – отмеченные точки. Нам требуется построить на прямых XY, YZ и ZX точки A, B и C соответственно так, чтобы в треугольнике ABC высота из A, биссектриса из B и медиана из C лежали соответственно на этих прямых.

  Выберем произвольную точку B' и проведём через неё прямую l₁, перпендикулярную XY; тогда  l₁ || BC  (см. рис.). Проведём через B' прямую, параллельную YZ, и отразим l₁ относительно этой прямой; мы получим прямую l₂, параллельную AB. На l₂ выберем произвольную точку A' и проведём через середину отрезка A'B' прямую, параллельную ZX, до пересечения с l₁ в точке C'. Построенный треугольник A'B'C' гомотетичен искомому (он переводится в ABC гомотетией, переводящей A' и B' в A и B соответственно; мы считаем параллельный перенос частным случаем гомотетии с бесконечно удалённым центром).

  Построим в этом треугольнике точкиX', Y' иZ', соответствующиеX, Y иZ соответственно. Из этих данных гомотетия однозначно восстанавливается, а после этого восстанавливается и исходный треугольник.

Ответ задачи отсутствует