Задача
В некотором государстве ценятся золотой и платиновый песок. Золото можно менять на платину, а платину на золото по курсу, который определяется натуральными числами g и p так: x граммов золотого песка равноценны y граммам платинового, если xp = yg (числа x и y могут быть нецелыми). Сейчас у банкира есть по килограмму золотого и платинового песка, а g = p = 1001. Государство обещает каждый день уменьшать одно из чисел g и p на единицу, так что через 2000 дней они оба станут единицами; но последовательность уменьшений неизвестна. Может ли банкир каждый день менять песок так, чтобы в конце гарантированно получить хотя бы по 2 кг каждого песка?
Решение
Докажем, что если вначале у банкира по 1 кг каждого песка, и g = p = k, то в конце хотя бы одного песка будет не больше 2 – 1/k кг. Для этого достаточно доказать, что если вначале у банкира по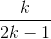 
кг песка, то в конце он не может получить каждого песка больше чем по килограмму.
Назовём состоянием банкира число S = Gp + Pg, если у него G кг золота и P кг платины. Заметим, что в результате обмена песка по курсу состояние не меняется. Покажем индукцией по числу дней, что наибольшее гарантированное состояние банкира в день, когда курсы равны g и p, не превосходит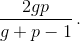 
В начальный день это так.
Пусть в некоторый день это так. Ясно, что при этом 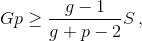либо 
либо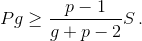 
(Оба неравенство выполнены одновременно только в случае, когда оба превращаются в равенства.)
Пусть выполнено первое неравенство, то есть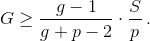 
Тогда государство уменьшит p на 1 (случай g > p = 1 будет разобран ниже). При этом из состояния вычтется G, то есть оно станет равно
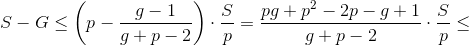
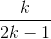
Ответ
Не может.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь