Задача
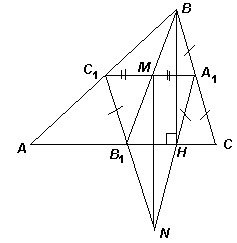
В треугольнике АВС проведены высота ВН, медиана ВВ1 и средняя линия А1С1 (А1 лежит на стороне ВС, С1 – на стороне АВ). Прямые А1С1 и ВВ1 пересекаются в точке М, а прямые С1В1 и А1Н – в точке N. Докажите, что прямые MN и BH параллельны.
Решение
Решение 1:
Пусть K – точка пересечения C1A1 и BH. Заметим, что MK и KA1 – средние линии треугольников B1BH и HBC соответственно. Следовательно,MK : KA1 = B1H : HC. Из параллельности прямых C1N и BC по теореме Фалеса получаем B1H : HC = NH : HA1. Итак, MK : KA1 = NH : HA1, откуда по обратной теореме Фалеса следует параллельность прямых MN и BH.
Решение 2:Так как А1С1 || AC, то М – середина отрезка А1С1 (см. рис.). Кроме того, С1В1 = ½ ВС = А1С = А1Н, поскольку НА1 – медиана прямоугольного треугольника ВНС. Таким образом, С1В1НА1 – равнобокая трапеция, откуда следует, что треугольник А1NС1 – равнобедренный. Поэтому его медиана NM является и высотой. Значит, MN ⊥ АС, то есть MN || BH.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь