Если P – параллелограмм, то нужно не менее четырёх гвоздей. Действительно, если некоторая его сторона не касается никакого гвоздя, то P можно двигать в направлении двух смежных с ней сторон.

  Покажем, что любой выпуклый многоугольник P можно зафиксировать четырьмя гвоздями.

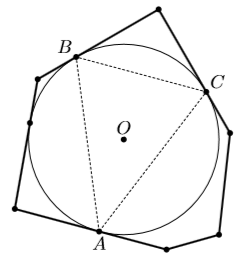
  Пусть окружность Ω с центром O – наибольшая из окружностей, лежащих внутри P, A₁, A₂, ..., A_k – точки касания Ω со сторонами P, H – выпуклая оболочка этих точек.

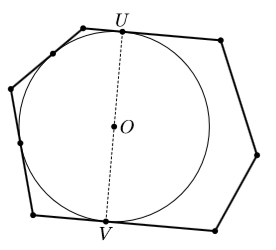
  Предположим, что существуют такие две вершины U и V многоугольника H, что UV – диаметр Ω (рис. слева). Вобьём два гвоздя в точки U и V. Очевидно, что стороны P, содержащие U и V, параллельны, следовательно, P можно двигать только в направлении, перпендикулярном UV. Чтобы зафиксировать P, достаточно вбить еще два гвоздя, препятствующие его движению влево и вправо от прямой UV.

  Теперь рассмотрим случай, когда стороны и диагоналиH не содержатO.   Предположим, что  O∉H.  ПустьPQ – сторонаH, разделяющаяH иO, а касательные к Ω в точкахP иQ пересекаются в точкеT. Тогда существует гомотетия с центромT и коэффициентом, большим 1, переводящая Ω в большую окружность, лежащую внутриP. Противоречие.   Таким образом,  O∈H.  Тогда существует треугольникABC, содержащийO (рис. справа). (A, B, C – точки касания Ω со сторонамиP.) Легко видеть, что три гвоздя, вбитые в точкиA, B иC, фиксируютP.

Ответ задачи отсутствует