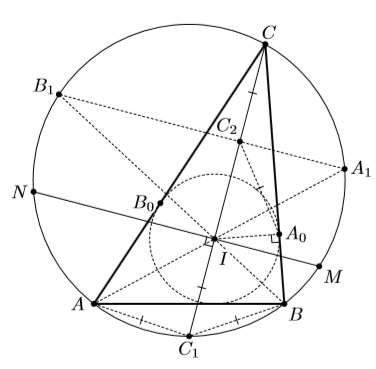
Решение 1:   Обозначим через A₁, B₁ и C₁ середины дуг BC, CA и AB, не содержащих других вершин треугольника ABC (рис. слева), через A₀ и B₀ – точки касания вписанной окружности со сторонами BC и CA соответственно, а через C₂ – точку пересечения A₁B₁ и CC₁.

  Пусть MN проходит через I. Так как A₁N и B₁M – диаметры, то хорды A₁B₁ и MN равны и параллельны. Ввиду очевидного равенства треугольников A₁CB₁ и A₁IB₁ прямая A₁B₁ – серединный перпендикуляр к отрезку CI. Из симметрии относительно серединного перпендикуляра к CC₁ имеем

CC₂ = C₁I,  кроме того, из прямоугольного треугольника CA₀I получим, что  C₂A₀ = C₂C.  По теореме о трезубце (см. задачу 153119)

C₂A₀ = C₂C = IC₁ = C₁A = C₁B.  Следовательно, треугольники C₂CA₀ и C₁AB равны и  AB = CA₀.  Отсюда и получаем равенство

AC + CB = AB₀ + B₀C + CA₀ + A₀B = 2AB + AB₀ + A₀B = 3AB.

  В обратную сторону доказательство аналогично.

         

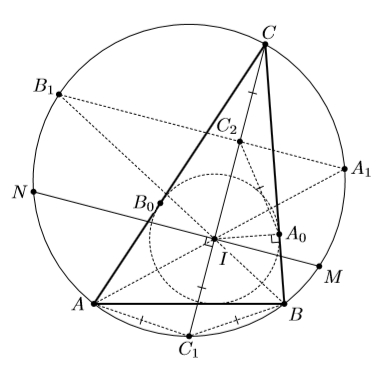
Решение 2:   Пусть J – центр вневписанной окружности, касающейся стороны AB (рис. справа). Заметим, что точки M и N являются центрами описанных окружностей треугольников ACJ и BCJ (этот вариант теоремы о трезубце также доказывается подсчётом углов). Следовательно, MN – серединный перпендикуляр к отрезку CJ, то есть I – середина CJ. Сделав гомотетию с центром C и коэффициентом ½, получим, что вписанная окружность касается средней линии треугольника ABC, параллельной AB. Условие описанности трапеции, образованной этой средней линией и сторонами, равносильно требуемому равенству.

  Обратное утверждение доказывается аналогично.

Ответ задачи отсутствует