Задача
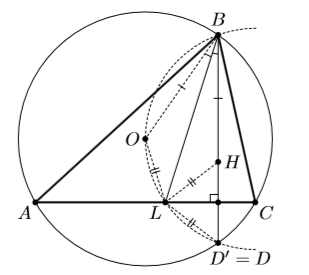
В треугольнике ABC ∠B = 60°, O – центр описанной окружности, BL – биссектриса. Описанная окружность треугольника BOL пересекает описанную окружность треугольника ABC вторично в точке D. Докажите, что BD ⊥ AC.
Решение
Пусть H – ортоцентр треугольника ABC. Точка D', симметричная H относительно AC лежит на описанной окружности (см. задачу 155463), а так как
∠B = 60°, то BO = BH (это следует из того, что треугольник, образованный вершиной B и основаниями высот, опущенных из вершин A и C, подобен треугольнику ABC с коэффициентом ½). Заметим, что луч BL – биссектриса угла OBH, поэтому LO = LH = LD'. Из симметрии относительно BL также следует, что ∠BOL = ∠BHL, а из симметрии относительно AC, что ∠BD'L = ∠LHD' = 180° – ∠BHL. Следовательно, четырёхугольник BOLD' – вписанный и D' совпадает с D.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь