Решение 1:Пусть M, N – середины AB, CD соответственно. Тогда степень точки K относительно окружности с диаметром AB равна  KM² – MA² = ¼ (CB² – AB²),  а относительно окружности с диаметром CD –  ¼ (AD² – CD²).  Так как  AB² + AD² = BD² = BC² + CD²,  эти степени равны, то есть точка K лежит на радикальной оси XY двух окружностей.

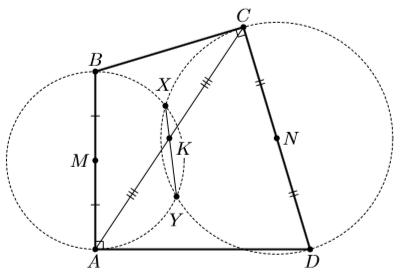
Решение 2:Пусть прямые AB и CD пересекаются в точке Z. Центры данных в условии окружностей ω₁ и ω₂ – середины M и N отрезков AB и CD. Пусть ω – окружность ABCD с диаметром BD. Тогда AB – радикальная ось окружностей ω и ω₁, CD – радикальная ось окружностей ω и ω₂, а XY – радикальная ось окружностей ω₁ и ω₂, значит XY проходит через Z. Теперь достаточно доказать, что  ZK ⊥ MN.  Но  MK || BC ⊥ ZN  и  NK || AD ⊥ ZM.  Следовательно, K – ортоцентр треугольника MZN, и  ZK ⊥ MN.

Ответ задачи отсутствует