Решение 1:   Без ограничения общности можно считать, что дуги ABC и BCD не превосходят полуокружности. Тогда

⌣AD = 2π – ⌣ABC – ⌣BCD + ⌣BC > ⌣BC.  Поскольку дуга ABC также больше дуги BC,  AD > BC.

  Теперь, если  AC > BD,  то  ⌣ABC > ⌣BCD,  ⌣AB > ⌣CD  и  AB > CD.

  При  AC < BD  все неравенства меняются на противоположные.

Решение 2:   Пусть AL – самый длинный из отрезков AL, BL, CL, DL (см. рис.). Тогда, в силу равенства  AL·CL = BL· DL,  CL – самый короткий из этих отрезков. Значит,  AL – CL > |BL – DL|,  откуда  AC² = (AL + CL)² = (AL – CL)² + 4AL·CL > |BL – DL|² + 4BL·DL = (BL + DL)² = BD²,  то есть  AC > BD.  Кроме того, из подобия треугольников ALB и DLC получаем, что  AB : CD = AL : DL,  то есть  AB > CD.  Аналогично из подобия треугольников ALD и BLC получаем

AD > BC.

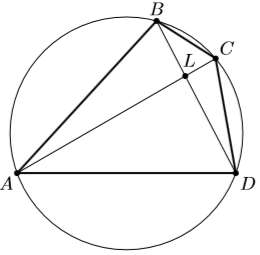
Решение 3:   AC = 2R sin B,  BD = 2R sin A,  поэтому неравенство  AC > BD  эквивалентно неравенству  sin B > sin A.

  (AD – BC)(AB – CD) > 0  ⇔  AD·AB + BC·CD > AD·CD + BC·AB,  что эквивалентно (домножим на  ½ sin A sin B = ½ sin A sin D = ½ sin C sin B)

Ответ задачи отсутствует