Задача
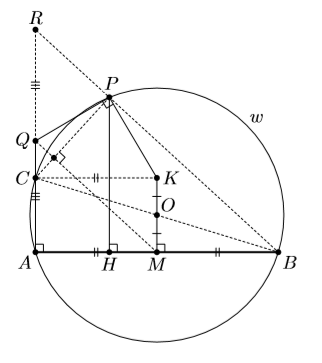
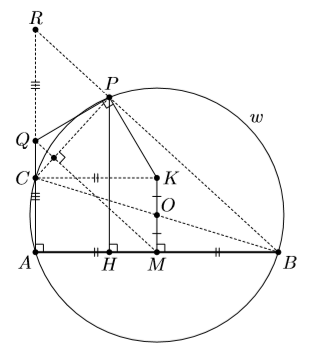
Пусть M – середина хорды AB окружности с центром O. Точка K симметрична M относительно O, P – произвольная точка окружности. Перпендикуляр к AB в точке A и перпендикуляр к PK в точке P пересекаются в точке Q. Точка H – проекция P на AB. Докажите, что прямая QB делит отрезок PH пополам.
Решение
Заметим, что ∠PBA ≠ 90° (иначе PK || AB, и точка Q не существует). Поэтому прямая BP пересекает AQ в некоторой точке R. Треугольники BPH и BRA гомотетичны, так что достаточно доказать, что Q – середина AR. Первый способ. Пусть прямая QA пересекает данную окружность в точке C, отличной от A (рис. слева). По условию отрезки BC и MK делят друг друга пополам, то есть CKBM – параллелограмм. Поскольку M – середина AB, то CKMA – прямоугольник.
MC² – MP² – QC² + QP² = (CK² + MK²) – (2PO² + 2OK² – PK²) – (QK² – CK²) + (QK² – PK²) =
= 2CK² + 4OK² – 2PO² – 2OK² = 2CK² + 2OK² – 2OC² = 0.
Значит, MQ ⊥ PC (см. задачу 157134). Так как CB – диаметр, BR ⊥ PC. Следовательно, MQ || BR, и поскольку M – середина AB, то Q – середина AR.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь