Задачи и олимпиады по математике

Задача

Дан треугольник с углами 30°, 70° и 80°. Разрежьте его отрезком на два треугольника так, чтобы биссектриса одного из этих треугольников и медиана второго, проведённые из концов разрезающего отрезка, были параллельны друг другу.

Решение

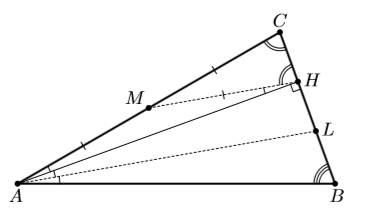
Пусть в треугольнике ABC ∠A = 30°, ∠B = 70°, ∠C = 80°, M – середина AC (см. рис.). Проведём высоту AH, а затем биссектрису AL треугольника HAB. Тогда ∠CAH = ∠MHA = 10° и ∠HAL = 10°. Значит, медиана треугольника AHC, проведённая из вершины H, и биссектриса треугольника BAH, проведённая из вершины A, параллельны.

Ответ

Ответ задачи отсутствует

Задача

Решение

Ответ

Подтверждение удаления