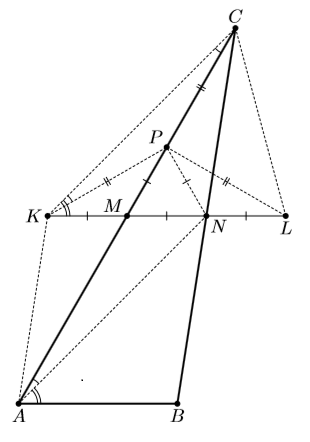
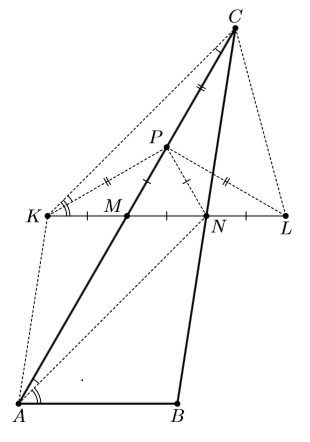
Решение 1:Продолжим отрезок MN на его длину в обе стороны и получим точки K и L (рис. слева). Так как M – общая середина отрезков AC и KN, то AKCN – параллелограмм. Значит,  ∠CKM = 45°,  ∠KCM = 15°.  Отметим на отрезке CM точку P так, чтобы угол CKP был равен 15°. Тогда отрезок KP разобьёт треугольник KCM на два равнобедренных треугольника. Кроме того,   ∠PMN = 60°,  поэтому треугольник MPN – равносторонний. Треугольники PLN и PKM равны, треугольник CPL – равнобедренный и прямоугольный, CLBM – параллелограмм, следовательно,  ∠ABM = ∠CLN = ∠CLP + ∠MLP = 75°.

               

Решение 2:Пусть G – точка пересечения медиан треугольника ABC, F – середина GB, треугольник GFO равносторонний, причём точки O и A лежат в одной полуплоскости относительно MB (рис. справа). Тогда  ∠MOB = 120° = 2∠MAB,  значит, O – центр описанной окружности треугольника MAB. При этом  ∠MOG = 30° = 2∠MAG,  поэтому лучи AG и OG проходят через одну точку описанной окружности треугольника AMB. Отсюда следует, что точки A, O и G лежат на одной прямой. Значит,  ∠AMB = ∠MOA : 2 = 75°.

75°.