Назад
Задача 164797 • Сложность: 2 • 8-10 класс
Задача

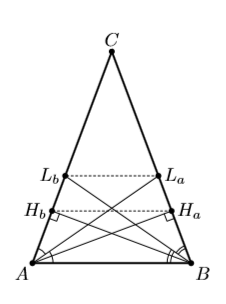
Пусть AHa и BHb – высоты, а ALa и BLb – биссектрисы треугольника ABC. Известно, что  HaHb || LaLb.  Верно ли, что  AC = BC?

Авторы:
Френкин Б. Р.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Олимпиада по геометрии имени И.Ф. Шарыгина X Олимпиада по геометрии имени И.Ф. Шарыгина (2014 г.)
Количество версий:
4
Решение

  Достаточно доказать,что  ∠LaBLb = ∠LbALa  (см. рис.). Это можно сделать по-разному.   Первый способ. Так как треугольники HaHbC и ABC подобны (см. задачу 152357), треугольники LaLbC и ABC также подобны, то есть

LaC : AC = LbC : BC.  Значит, подобны треугольники ALaC и BLbC. Следовательно,  ∠LaBLb = ∠LbALa.

 Второй способ. Так как прямыеHaHbиABантипараллельны относительно прямыхACиBC, прямыеLaLbиABтакже антипараллельны относительноACиBC. Значит, четырёхугольникALbLaB– вписанный, и  ∠LaBLb= ∠LbALa.

Ответ

Верно.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет