Домножив, если нужно, числа a и b на подходящую степень десятки, мы можем считать, что десятичные записи чисел  a, b,  a – b  и  a + kb  – чисто периодические (то есть периоды начинаются сразу после запятой).

  Тогда 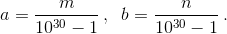    Нам также известно, что числа  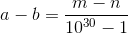   и 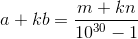    записываются десятичными дробями с периодом длины 15, то есть могут быть записаны как обыкновенные дроби со знаменателем  10¹⁵ – 1.  Поэтому так может быть записана и их разность  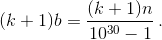   Таким образом, число  (k + 1)n  делится на  10¹⁵ + 1,  а число n – не делится (иначе и b записывалось бы дробью с периодом длины 15). Значит, число  k + 1  делится на некоторый простой делитель числа  10¹⁵ + 1.  Наименьший из таких делителей – это 7. Действительно, число  10¹⁵ + 1  не делится ни на 2, ни на 5 и даёт остаток 2 при делении на 3. С другой стороны, оно делится на  10³ + 1 = 7·143.  Итак,  k + 1 ≥ 7,  то есть  k ≥ 6.   Пусть  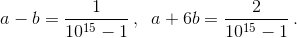   Тогда 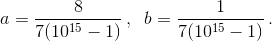    Ясно, что длины минимальных периодов чисел

a – b  и  a + 6b  равны 15. Длины минимальных периодов чисел a и b больше 15 и делятся на 15 (так как  10^T – 1  должно делиться на  10¹⁵ – 1).  С другой стороны, так как  10³⁰ – 1  делится на   7(10¹⁵ – 1),  числа a и b периодичны с длиной периода 30. Значит, длины их минимальных периодов равны 30.

При  k = 6.