Лемма. Рассмотрим треугольники ABC и A'B'C', вписанные в окружность Ω; пусть их соответствующие стороны пересекаются в точках A₁, B₁, C₁. Тогда 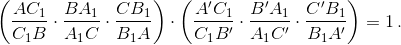    Доказательство. Из подобия треугольников AC₁A' и B'C₁B имеем  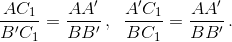   Перемножая эти равенства с четырьмя аналогичными, получаем требуемое.   Докажем сначала, что для любых точек A₁, B₁ на сторонах BC и AC найдётся не более одной точки C₁ на стороне AB, для которой треугольник ABC восстанавливается однозначно. Зафиксируем треугольник ABC и точки A₁, B₁. Пусть A₂, B₂ – вторые точки пересечения прямых AA₁, BB₁ с окружностью Ω; C' – произвольная точка дуги A₂CB₂; A', B' – вторые точки пересечения прямых C'A₁, C'B₁ с Ω; C₁ – точка пересечения AB и A'B'. Когда точка C' близка к A₂ или к B₂, точка C₁ близка к A или B соответственно. При движении точки C' от A₂ до B₂ точка C₁ непрерывно движется от A до B (в случае, когда

C = C',  рассматривается предельное положение точки C₂; то, что оно существует, гарантируется леммой). Значит, для любой точки C₁, кроме, возможно, вышеупомянутого предельного положения, треугольник ABC однозначно не восстанавливается, ибо существует второй треугольник A'B'C'.

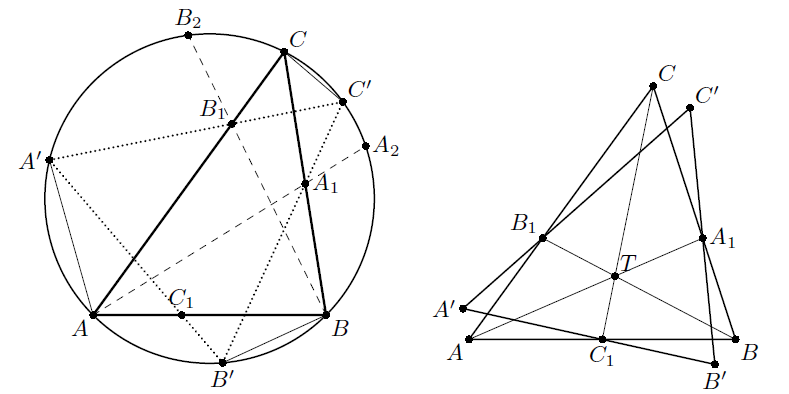
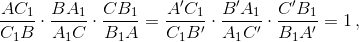  Осталось доказать, что, еслиAA₁,BB₁,CC₁пересекаются в одной точкеT, то треугольник восстанавливается однозначно (тогда из вышедоказанного следует, что других случаев нет). Пусть это не так; тогда из леммы получаем    то есть отрезкиA'A₁,B'B₁,C'C₁также пересекаются в одной точкеT', что невозможно. Действительно, пусть, например, точкаA'лежит на дугеAC; тогдаT'не может лежать в углеATB, так как его не пересекает отрезокA'A₁. Остальные случаи разбираются аналогично.

Ответ задачи отсутствует