Задача
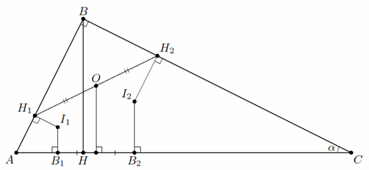
В прямоугольном треугольнике ABC (∠B = 90°) проведена высота BH. Окружность, вписанная в треугольник ABH, касается сторон AB, AH в точках H1, B1 соответственно; окружность, вписанная в треугольник CBH, касается сторон CB, CH в точках H2, B2 соответственно. Пусть O – центр описанной окружности треугольника H1BH2. Докажите, что OB1 = OB2.
Решение
Обозначим γ = ∠ACB. Пусть I1, I2 – центры вписанных окружностей треугольников ABH, CBH. Из подобия этих треугольников следует, что
I1H1 : I2H2 = AB : BC = tg γ. Так как отрезки I1H1, I2H2 перпендикулярны соответственно AB и BC, то проекции этих отрезков на AC равны I1H1 cos γ и I2H2 sin γ, то есть равны друг другу. Тогда, поскольку O – середина H1H2, то проекция O на AC совпадает с серединой B1B2, что равносильно утверждению задачи.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь