Центральными кониками будем называть эллипсы и гиперболы.   Лемма. Две различные центральные коники с общим центром O имеют не более четырёх общих касательных.

  Доказательство. Будем считать, что O – начало координат. Если одна из коник – эллипс, превратим его в окружность, проведя сжатие к O вдоль его большой оси. Осталось доказать, что вторая коника имеет не более четырёх касательных, удаленных от O на радиус этой окружности. Вершины делят эту конику на четыре куска. Очевидно, что при движении точки касания по каждому куску расстояние от касательной до центра коники O меняется монотонно. Следовательно, принимать данное значение это расстояние может не более одного раза.

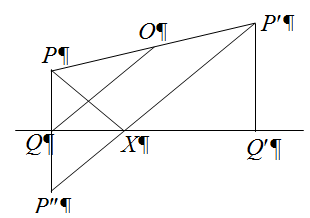
  Если обе коники – гиперболы, проведём проективное преобразование  (x, y) → (¹/_x, ^y/_x).  При этом обе гиперболы превратятся в эллипсы, а их общий центр, как легко проверить, останется в точке O. Таким образом, этот случай сводится к предыдущему.   Пусть проекции точки P на стороны лежат на окружности радиуса r с центром O, а P' – точка, симметричная P относительно O. Тогда проекции P' на стороны лежат на той же окружности. Рассмотрим случай, когда точка P лежит внутри этой окружности, и докажем, что эллипс, заданный условием  XP + XP' = 2r,  касается всех сторон четырёхугольника. Пусть q, Q' – проекции точек P, P' на одну из сторон, точка P'' симметрична P относительно прямой QQ', а X – точка пересечения QQ' и P'P'' (см. рис). Тогда  XP + XP' = XP'' + XP' = P''P' = 2Q'O = 2r,  то есть точка принадлежит указанному эллипсу. С другой стороны, любая другая точка Y прямой QQ' лежит вне эллипса (поскольку  YP + YP' = YP'' + YP' > P''P = 2r).  Это и значит, что эллипс касается прямой QQ', содержащей сторону четырёхугольника.

  Если точка лежит вне нашей окружности, то аналогично доказывается, что всех сторон четырёхугольника касается гипербола, заданная условием |XP – XP'| = 2r.   Итак, стороны четырёхугольника являются общими касательными к двум коникам с общим центром. По лемме таких касательных может быть не больше четырёх, и они разбиваются на две пары симметричных (а значит, параллельных). Следовательно, стороны четырёхугольника и являются этими четырьмя касательными, то есть образуют параллелограмм.

Ответ задачи отсутствует