Задача
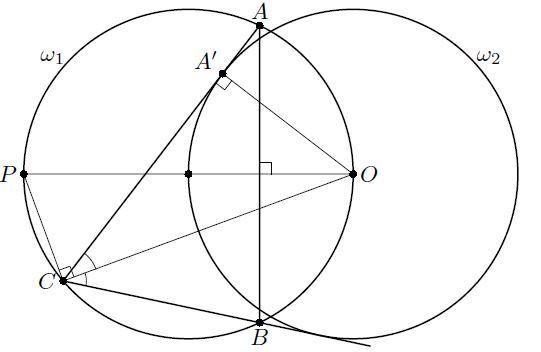
Каждая из двух равных окружностей ω1 и ω2 проходит через центр другой. Треугольник ABC вписан в ω1, а прямые AC, BC касаются ω2.
Докажите, что cos∠A + cos∠B = 1.
Решение
Пусть R – радиус окружностей, O – центр ω2, P – точка на ω1, диаметрально противоположная к O, а A' – точка касания AC и ω2. Так как CO – биссектриса угла ACB, точки A и B симметричны относительно прямой OP.
Заменим сумму косинусов произведением: cos∠A + cos∠B = 2 sin(½ ∠C) cos(½ (∠A – ∠B)). Из отмеченной выше симметрии следует, что
½ |∠A – ∠B| = ∠OCP, то есть OP cos(½ (∠A – ∠B)) = CO. Поскольку ½ ∠C = ∠OCA = ∠OCA', то CO sin (½ ∠C) = OA' = R = OP/2. Итак,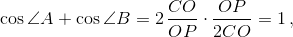 
что и требовалось.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет