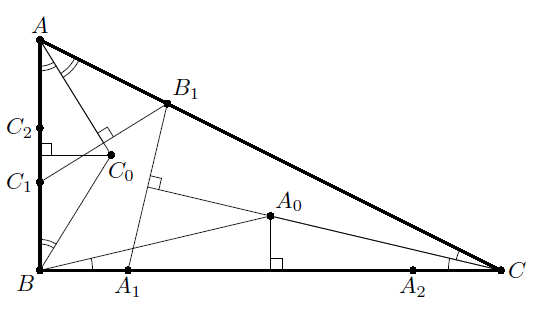
Задача
Окружность, вписанная в прямоугольный треугольник ABC (∠ABC = 90°), касается сторон AB, BC, AC в точках C1, A1, B1 соответственно. Вневписанная окружность касается стороны BC в точке A2. A0 – центр окружности, описанной около треугольника A1A2B1; аналогично определяется точка C0. Найдите угол A0BC0.
Решение
Поскольку точки A1 и A2 симметричны относительно середины отрезка BC (см. задачу 155404), то A0B = A0C. С другой стороны, A0 лежит на серединном перпендикуляре к отрезку A1B1, который совпадает с биссектрисой угла C. Следовательно, ∠CBA0 = ∠A0CB = ½ ∠C. Аналогично
∠ABC0 = ½ ∠A, и, значит, ∠A0BC0 = ∠B – ½ (∠C + ∠A) = 45°.
Ответ
45°.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет