Задача
На прямой лежат точки X, Y, Z (именно в таком порядке). Треугольники XAB, YBC, ZCD – правильные, причём вершины первого и третьего ориентированы против часовой стрелки, а второго по часовой стрелке. Докажите, что прямые AC, BD и XY пересекаются в одной точке.
Решение
Через ∠(k, l) будем обозначать направленный угол между прямыми k и l (считающийся против часовой стрелки).
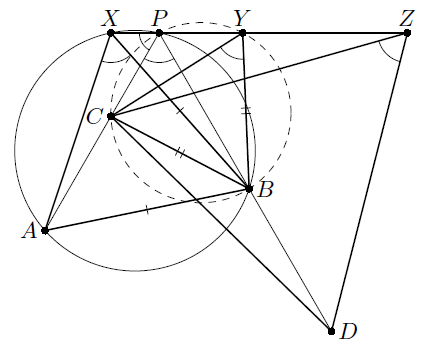
При повороте на 60° по часовой стрелке вокруг B точки A и C переходят соответственно в X и Y. Следовательно, ∠(XY, AC) = 60°. Пусть P – точка пересечения прямых XY и AC. Тогда ∠(XP, AP) = 60° = ∠(XB, AB), то есть точки A, X, P, B лежат на одной окружности. Отсюда
∠(CP, PB) = ∠(AX, XB) = 60° = ∠(CY, YB), то есть точки B, C, P, Y также лежат на одной окружности. Таким образом, точка P является второй точкой пересечения прямой XZ и описанной окружности треугольника BCY. Аналогично показывается, что прямая BD также проходит через эту точку. (В случае, если эти окружность и прямая касаются, P совпадает с Y, и все три прямые проходят через Y.)
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь