Задача
Радикалом натурального числа N (обозначается rad(N)) называется произведение всех простых делителей числа N, взятых по одному разу. Например,
rad(120) = 2·3·5 = 30. Существует ли такая тройка попарно взаимно простых натуральных чисел A, B, C, что A + B = C и C > 1000 rad(ABC)?
Решение
Будем искать пример в виде C = 10n, B = 1, A = 10n – 1.
Индукцией по k докажем, что для любого натурального k существует такое натуральное n, что 10n – 1 кратно 3k+1.
База: 101 – 1 кратно 32.
Шаг индукции. Если 10n – 1 кратно 3k+1, то 103n – 1 = (10n – 1)(102n + 10n + 1) кратно 3k+2, так как 102n + 10n + 1 делится на 3.
Возьмём теперь такое k, что 3k > 10000, и такое n, что 10n – 1 кратно 3k+1. Тогда
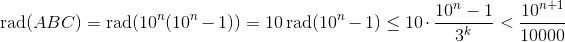
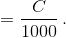
Ответ
Существует.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь