Пусть Петя первым ходом заменит 2015 на 2014, а каждым следующим ходом будет уравнивать числа (он всегда может это сделать, повторив ход Васи с тем числом, которое Вася не менял):

  Если Петя будет действовать так всю игру, то, конечно, в некоторый момент Вася сделает из одного из двух одинаковых чисел однозначное и выиграет.

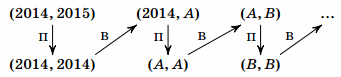
  Но посмотрим на этот момент внимательнее. Если Вася выиграл, заменив в паре (X, X)одно из двух чисел X на однозначное, то перед этим, на ходу Пети, число X на доске уже было. В этот момент Петя может заменить X на однозначное число и выиграть:

  (Петя может так пойти, потому что у него есть все возможности, которые были у Васи на последнем, выигрышном ходе: делить число X пополам, если оно чётное, и вычитать из него его же цифру.)

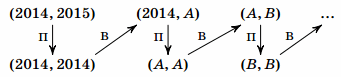
  Итак, сформулируем стратегию Пети полностью: "если одно из чисел можно заменить на однозначное – сделать это; в противном случае уравнять два числа".

Петя.