Задача
Дана правильная треугольная пирамида SABC, ребро основания которой равно 1. Из вершин A и B основания ABC проведены медианы боковых граней, не имеющие общих точек. Известно, что на прямых, содержащих эти медианы, лежат рёбра некоторого куба. Найдите длину бокового ребра пирамиды.
Решение
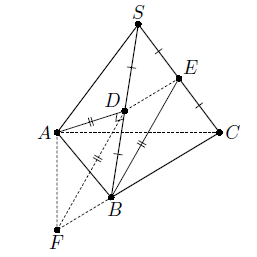
Указанные медианы AD и BE боковых граней ASB и BSC лежат на скрещивающихся прямых, а скрещивающиеся рёбра куба взаимно перпендикулярны. Таким образом, требуется найти длину b бокового ребра пирамиды, у которой угол между скрещивающимися медианами боковых граней равен 90°. Первый способ. По формуле для вычисления медианы треугольника  . При параллельном переносе на вектор
. При параллельном переносе на вектор 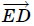 образом медианы BE является отрезок FD (точка F лежит на прямой BC, см. рис.). Из треугольника ABF по теореме косинусов
образом медианы BE является отрезок FD (точка F лежит на прямой BC, см. рис.). Из треугольника ABF по теореме косинусов 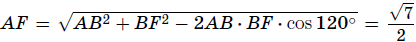 . Треугольник ADF – прямоугольный равнобедренный, поэтому
. Треугольник ADF – прямоугольный равнобедренный, поэтому 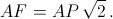 Значит,
Значит, 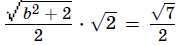 , откуда
, откуда 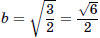 .
.
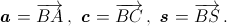 Имеем:
Имеем: 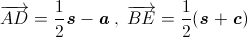 (см. рис.). Отсюда
(см. рис.). Отсюда 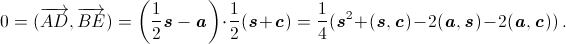 Учитывая, что BA = BC = 1 и BS = b, получим: 0 = ¼ (b² + b·1·cos α – 2b·1 – 2·1·1·cos 60°) = ¼ (b² – b cos α – 1).
Учитывая, что BA = BC = 1 и BS = b, получим: 0 = ¼ (b² + b·1·cos α – 2b·1 – 2·1·1·cos 60°) = ¼ (b² – b cos α – 1). 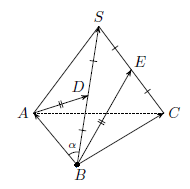
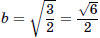 .
.
Ответ
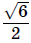 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь