Задача
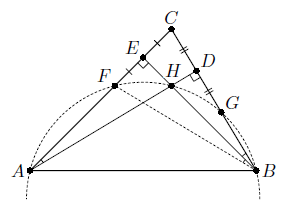
Высоты AD и BE остроугольного треугольника ABC пересекаются в точке H. Описанная окружность треугольника ABH, пересекает стороны AC и BC в точках F и G соответственно. Найдите FG, если DE = 5 см.
Решение
Пусть ∠FAH = ∠HBF = α. Прямоугольные треугольники ADC и ECB имеют общий угол C, поэтому ∠EBC = α.
Таким образом, BE – высота и биссектриса треугольника FBC, следовательно, этот треугольник равнобедренный и BE является его медианой, то есть
FE = EC. Аналогично CD = DG. Значит, ED – средняя линия треугольника FCG. Поэтому FG = 2DE.
Ответ
10 см.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет