Задача
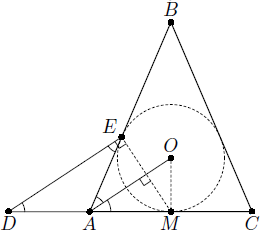
В равнобедренный треугольник ABC (AB = BC) вписана окружность с центром O, которая касается стороны AB в точке E. На продолжении стороны AC за точку A выбрана точка D так, что AD = ½ AC. Докажите, что прямые DE и AO параллельны.
Решение
Пусть M – точка касания окружности со стороной AC (см. рис.). Так как треугольник ABC – равнобедренный, то M – середина AC. Таким образом,
DA = AM = MC.
С другой стороны, AE = AM (отрезки касательных, проведённых к окружности из одной точки). Из равенства AE = AM = AD следует, что треугольник DEM – прямоугольный с прямым углом E, то есть DE ⊥ EM. Кроме того, в равнобедренном треугольнике EAM биссектриса AO является также высотой, то есть AO ⊥ EM. Следовательно, DE и AO параллельны.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь