Из условия следует, что  ∠BMA = ∠CMK = 60°,  а тогда и  ∠AMK = 60° (рис. слева). Далее можно рассуждать по-разному.   Первый способ. Пусть AH – перпендикуляр, опущенный из вершины A на MK. Тогда прямоугольные треугольники AMB и AMH равны по гипотенузе и острому углу, откуда  AH = AB.  Если точка H лежит на отрезке MK, то прямоугольные треугольники AKH и AKD равны по гипотенузе и катету. Следовательно,  ∠AKD = ½ ∠MKD = 75°.

  Если H лежит на продолжении отрезка MK за точку K, то отрезок AH пересекает сторону CD в точке X. Но тогда  AH > AX > AD,  что противоречит равенству  AH = AD.

  Второй способ. Диагональ CA квадрата является биссектрисой внутреннего угла треугольника CMK, а луч MA – биссектрисой его внешнего угла, поэтому вершина A – центр вневписанной окружности этого треугольника. Следовательно, KA также является биссектрисой внешнего угла треугольника CMK, поэтому  ∠AKD = ½ ∠MKD = 75°.   Третий способ. Продлим отрезок KM до пересечения с прямой AB в точке P (рис. справа). Тогда  ∠PMB = ∠CMK = ∠AMB.  Следовательно, прямоугольные треугольники PMB и AMB равны (по катету и острому углу), то есть  AP = 2a,  где a – сторона данного квадрата, и  PM = AM.

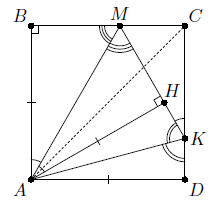
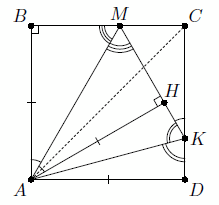
  По свойству катета, противолежащего углу в 30°,  AM = 2BM  и  MK = 2MC.  Следовательно,  PK = PM + MK = 2(BM + MC) = 2BC = 2a.

  Таким образом, треугольник APK – равнобедренный с углом 30° при вершине P, поэтому угол MKA при его основании равен 75°, а

∠AKD = 180° – 30° – 75°.

75°.