Задача
В параллелограмме ABCD из вершины тупого угла B проведены высоты BM и BN, а из вершины D – высоты DP и DQ.
Докажите, что точки M, N, P и Q являются вершинами прямоугольника.
Решение
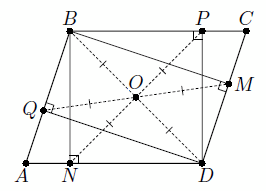
Пусть, для определённости, точка N лежит на прямой AD, а точка Q – на прямой AB (см. рис.). Тогда диагонали BD и PN прямоугольника PBND равны и пересекаются в их общей середине O. Аналогично, диагонали BD и QM прямоугольника QBMD равны и пересекаются в их общей середине O. Значит, и диагонали PN и QM четырёхугольника PQNM равны и пересекаются в их общей середине O. Следовательно, PQNM – прямоугольник.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет