Так как АС – серединный перпендикуляр к отрезку BB', то центр О_В описанной окружности Ω_B треугольника АВВ' лежит на прямой АС. Аналогично, центр О_С описанной окружности Ω_C треугольника ACC' лежит на прямой АВ (см. рис.).

  Проведем описанную окружность Ω треугольника АВС. Общей хордой Ω и Ω_B является отрезок АВ, поэтому линия центров ОО_В является серединным перпендикуляром к АВ. Аналогично ОО_С – серединный перпендикуляр к стороне АС. Обозначив точки пересечения ОО_В с АВ и ОО_С с АС через С₀ и В₀ соответственно, получим, что О_ВС₀ и О_СВ₀ – высоты треугольника АО_ВО_С, а точка О их пересечения – ортоцентр этого треугольника.

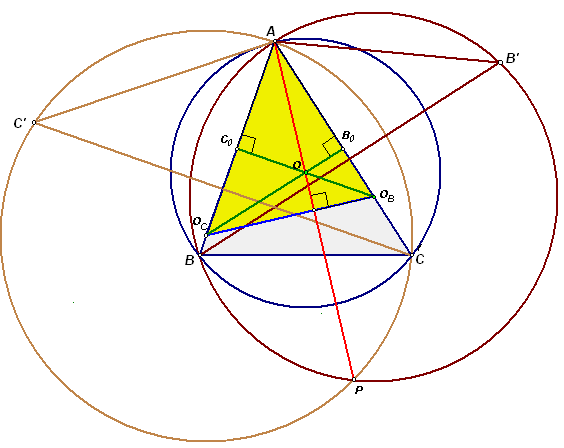
  Отрезок АР – общая хорда Ω_B и Ω_C, значит, он перпендикулярен их линии центров О_ВО_С. Следовательно, прямая АР содержит третью высоту треугольника АО_ВО_С и поэтому проходит через точку О.

Ответ задачи отсутствует