Задача
Сеть автобусных маршрутов в пригороде Амстердама устроена так, что:
а) на каждом маршруте есть ровно три остановки;
б) каждые два маршрута либо вовсе не имеют общих остановок, либо имеют только одну общую остановку.
Какое наибольшее количество маршрутов может быть в этом пригороде, если в нём всего 9 остановок?
Решение
Оценка. Рассмотрим какую-нибудь остановку A. Определим наибольшее количество маршрутов, проходящих через неё. Кроме A, в городе еще 8 остановок. На каждом маршруте, проходящем через A, есть ещё две остановки. Так как никакие два из этих маршрутов не могут иметь общих остановок, отличных от A, то всего через A может проходить не более, чем 8 : 2 = 4 маршрута. Занумеруем все остановки и обозначим через a1 количество маршрутов, проходящих через первую остановку, через a2 количество маршрутов, проходящих через вторую остановку, ..., через a9 количество маршрутов, проходящих через девятую остановку. Так как на каждом маршруте ровно 3 остановки, то a1 + ... + a9 = 3n, где n – общее количество маршрутов. По доказанному выше, каждое слагаемое не больше четырёх. Следовательно, 3n < 4·9 = 36, то есть n < 12.
Пример. На рисунке изображена схема, удовлетворяющая условию задачи и содержащая 12 маршрутов.
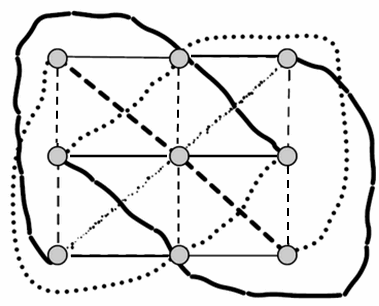
Ответ
12 маршрутов.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь