Задача
Найдите сумму Sl(x) = g0,l(x) – g1,l–1(x) + g2,l–2(x) – ... + (–1)lgl,0(x).
Определение многочленов Гаусса gk,l(x) можно найти в справочнике.
Решение
Из задачи 161522 в) следует, что Sl(x) = (1 – xl–1)g0,l–1(x) – (1 – xl–2)g1,l–2(x) + ... + (–1)l–1(1 – x0)gl–1,0(x). Применяя очевидное равенство
(1 – xm)gk,m(x) = (1 – xk+m)gk,m–1(x) к каждому слагаемому в последней сумме, приходим к равенству Sl(x) = (1 – xl–1)Sl–2(x).
Поскольку S1(x) = 0, отсюда следует, что Sl(x) = 0 для каждого нечётного l.
S0(x) = 1, поэтому для чётного l = 2n получаем 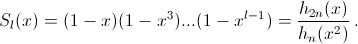
Ответ
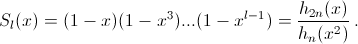
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет