Задача
Функции a, b и c заданы рядами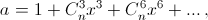 
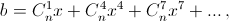
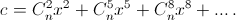Докажите, что a³ +b³ +c³ – 3abc= (1 +x³)n.
Решение
Заметим, что a³ + b³ + c³ – 3abc = (a + b + c)(a + ωb + ω²c)(a + ω²b + ωc) (см. задачу 161259). Имеем
a + b + c = (1 + x)n,
a + ωb + ω²c = (1 + ωx)n,
a + ω²b + ωc = (1 + ω²x)n.
Поэтому a³ + b³ + c³ – 3abc = ((1 + x)(1 + ωx)(1 + ω²x))n = (1 + x³)n.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет