Пусть  f(x) = β_kx^k + β_k–1x^k–1 + ... + β₁x + β₀  – многочлен. Для последовательности  (a) = (a₀, a₁, a₂, ...)  через  f(a) будем обозначать последовательность, n-й член которой равен  β_ka_n+k + β_k–1a_n+k–1 + ... + β₁a_n+1 + β₀a_n.  Если  f – характеристический многочлен рекуррентной последовательности (a) k-го порядка, то  f(a) = (0).

  Легко проверить, что  (αf)(a) = αf(a),  (f + g)(a) = f(a) + g(a),  (fg)(a) = f(g(a)).   Лемма. Если  f = gh,  где многочлены g и h взаимно просты, то  f(a) = 0  тогда и только тогда, когда  (a) = (b) + (c),  где  g(b) = 0  и  h(с) = 0.

  Доказательство. ⇐.  f(a) = hg(b) + gh(c) = h(0) + g(0) = (0).

  ⇒. Согласно задаче 160990 найдутся такие многочлены u и v, что  g(x)u(x) + h(x)v(x) = 1.  Положим  (b) = hv(a),  (c) = gu(a),  тогда

g(b) = vf(a) = 0,  h(c) = vf(a) = 0,  (a) = (b) + (c).   б) Достаточно найти общий вид рекуррентной последовательности (a) с характеристическим многочленом  f(x) = (x – q)^α,  где  q ≠ 0,  а потом применить лемму.

  Докажем, что  a_n = g(n)qⁿ,  где g – произвольный многочлен степени не выше  α – 1.

  Пусть  a_n = g(n)qⁿ  для всех n. Обозначим  h(x) = x – q,  тогда  f = h^α.  Заметим, что n-й член последовательности h(a) равен

g(n + 1)qⁿ⁺¹ – qg(n)qⁿ = Δg(n)qⁿ⁺¹.  Поэтому n-й член последовательности  f(a) равен  Δ^αg(n)q^n+α = 0,  так как согласно задаче 161437  Δ^αg = 0.

  Пусть  f(a) = (0).  Последовательность (a) полностью определяется начальными условиями  a₀, ..., a_α–1.  Поэтому достаточно подобрать такой многочлен g степени  α – 1,  что  a₀ = g(0),  a₁ = g(1)q,  ...,   a_α–1 = g(α – 1)q^α–1.  Но такой многочлен существует (и единственен) – см. задачу 161052.

а)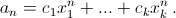  

б) 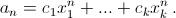    где g_i – многочлен степени не выше  α_i – 1.