а) Нетрудно понять, что F_n – приведённый многочлен степени  n – 1,  причём при (не)чётном n коэффициенты при (не)чётных степенях x этого многочлена равны нулю. Пусть 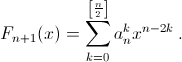    Тогда из равенства  F_n+1(x) = xF_n + F_n–1(x)  получаем  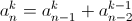   (мы считаем  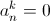   при

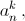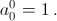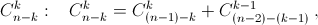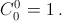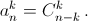k < 0  и  k > ⁿ/₂).  Это соотношение позволяет найти все   &nbsp зная   &nbsp Но такому же рекуррентному соотношению удовлетворяют и биномиальные коэффициенты     причём   &nbsp Значит,   &nbsp   Заметим, что  L_n(x) = 2F_n+1(x) – xF_n(x).  Действительно многочлены справа удовлетворяют как начальным условиям, так и рекуррентному соотношению для многочленов Люка. Поэтому

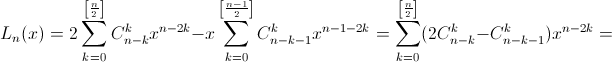
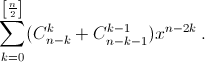
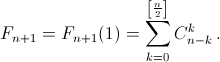  б) Числа F_n(1) удовлетворяют определению последовательности Фибоначчи. Поэтому     В задаче 60582 фактически требуется найти числа  S_n = (–1)ⁿF_n+1(–1).  Эта последовательность удовлетворяет начальным условиям  S₀ = S₁ = 1  и рекуррентному соотношению  S_n+1 = S_n – S_n–1.  Нетрудно проверить, что она периодическая с периодом 6.

а)