Задача
а) Пусть q – натуральное число и функция f(x) = cqx + anxn + ... + a1x + a0 принимает целые значения при x = 0, 1, 2, ..., n + 1.
Докажите, что при любом натуральном x число f(x) также будет целым.
б) Пусть выполняются условия пункта а) и f(x) делится на некоторое целое m ≥ 1 при x = 0, 1, 2, ..., n + 1. Докажите, что f(x) делится на m при всех натуральных x.
Решение
а) Рассмотрим многочлены P(x) =f(x) –cqx и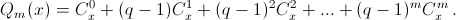 
Заметим, что
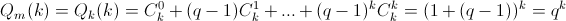при k= 0, 1, ...,m. В частности, f(x) совпадает с P(x) +сQn(x) в точках
0, 1, 2, ...,n. Согласно задаче161451многочленn-й степени Rn(x) =P(x) +сQn(x) принимает целые значения во всех целых точках. Но по тем же соображениям это верно и для многочлена Rn+1(x) =P(x) +сQn+1(x). Значит, и разность 
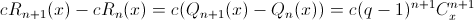будет целой при всех целыхx. В частности, число 
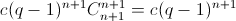– целое. Тем более целыми будут числа c(q– 1)n+m и 
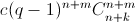при натуральныхk, m ≤ k. Таким образом, 
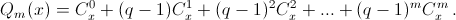– целое число.
б) Достаточно заметить, что функция 1/mf(x) удовлетворяет условиям пункта а).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь