Задача
Решите системы уравнений: а) x1 + x2 + x3 = 0,
x2 + x3 + x4 = 0,
  ...
x99 + x100 + x1 = 0,
x100 + x1 + x2 = 0; б) x + y + z = a,
y + z + t = b,
y + z + t = c,
t + x + y = d; в)   x1 + x2 + x3 + x4 = 2a1,
x1 + x2 – x3 – x4 = 2a2,
x1 – x2 + x3 – x4 = 2a3,
x1 – x2 – x3 + x4 = 2a4; г)   x1 + 2x2 + 3x3 + ... + nxn = a1,
nx1 + x2 + 2x3 + ... + (n – 1)nxn = a2,
...
2x1 + 3x2 + 4x3 + ... + xn = an.
Решение
а) Вычитая из второго уравнения первое, получим x4 = x1. Аналогично, x5 = x2, x6 = x3, ..., x3 = x100. Так как 100 не делится на 3 отсюда следует, что
x1 = x2 = x3 = ... = x100. б) Сложив все уравнения, получим x + y + z + t = 1/3 (a + b + c + d). Вычитая отсюда каждое из уравнений, получим ответ. в) Сложив все уравнения, получим 4x1 = 2(a1 + a2 + a3 + a4). Сложив первые два уравнения и вычтя из результата два последних, аналогично найдём x2. И так далее. г) Обозначим s = x1 + x2 + ... + xn. Сложив все уравнения, получим ½ n(n + 1)s = a1 + a2 + ... + an. Вычитая из первого уравнения второе, получим s – nx1 = a1 – a2. Отсюда x1 = 1/n (s – a1 + a2). Аналогично находятся остальные неизвестные.
Ответ
а) (0, 0, ..., 0). б) x = 1/3 (a + b + c – 2d), y = 1/3 (a + b – 2c + d), z = 1/3 (a – 2b + c + d), t = 1/3 (b + c + d – 2a). в) x1 = ½ (a1 + a2 + a3 + a4), x2 = ½ (a1 + a2 – a3 – a4), x3 = ½ (a1 – a2 + a3 – a4), x4 = ½ (a1 – a2 – a3 + a4). г) 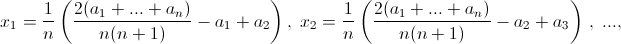
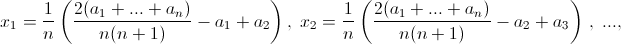
Чтобы оставлять комментарии, войдите или зарегистрируйтесь