Задача
Исследуйте системы уравнений: а) ![]()
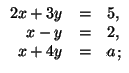 б)
б) ![]()
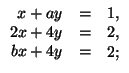 в)
в) ![]()
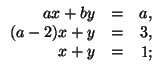 г)
г) ![]()
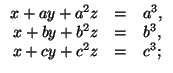 д)
д) ![]()
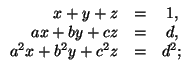 е)
е) ![]()
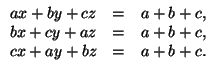
Решение
г) Рассмотрим приведённый многочлен f(t) = t3 – zt² – yt – x. a, b, c – его корни.
Если a, b, c – различные числа, то f(t) = (t – a)(t – b)(t – c), то есть x = abc, y = – (ab + bc + ca), z = a + b + c.
Пусть c = a ≠ b. Тогда f(t) = (t – a)(t – b)(t – u), где u – произвольное число. Значит, x = abu, y = – ab – u(a + b), z = a + b + u.
В случае a = b = c ответ можно выписать сразу: x = a(a² – y – az). е) После замены u = x – 1, v = y – 1, w = z – 1 система приобретает геометрический смысл: вектор (u, v, w) ортогонален векторам
(a, b, c), (b, c, a), (c, a, b). Если последние три вектора некомпланарны, то (u, v, w) = (0, 0, 0). Нетрудно видеть, что компланарны эти векторы в двух случаях: a + b + c = 0 или a = b = c. Каждый из этих случаев легко разбирается: в первом случае (u, v, w) = t(1, 1, 1), во втором u + v + w = 0.
Ответ
а) При a = 3 x = 2,2, y = 0,2; при a ≠ 3 решений нет. б) При a ≠ 2, b = 2 x = 1, y = 0; при a = 2, b ≠ 2 x = 0, y = ½; при a = b = 2 x = 1 – 2y; при a ≠ 2, b ≠ 2 решений нет. в) При a = 5 x = 1, y = 0; при a = b ≠ 3, 5 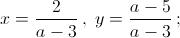 при a = 3 и при a ≠ 5, b ≠ a решений нет. г) Если a, b, c – различные числа, то x = abc, y = – (ab + bc + ca), z = a + b + c; при a ≠ b, c = a или b x = abu, y = – ab – u(a + b),
при a = 3 и при a ≠ 5, b ≠ a решений нет. г) Если a, b, c – различные числа, то x = abc, y = – (ab + bc + ca), z = a + b + c; при a ≠ b, c = a или b x = abu, y = – ab – u(a + b),
z = a + b + u, где u – произвольное число; при a = b ≠ c x = acu, y = – ac – u(a + c), z = a + c + u, где u – произвольное число;
при a = b = c x = a(a² – y – az). д) Если a, b, c – различные числа, то 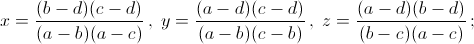
при a = b ≠ c, если d = a, то y = 1 – x, z = 0, если d = c, то y = – x, z = 1, если d не равно ни a, ни c, то решений нет;
при a = c ≠ b, если d = a, то y = 0, z = 1 – x, если d = b, то y = 1, z = – x, если d не равно ни a, ни b, то решений нет;
при b = c ≠ a, если d = a, то x = 1, z = – y, если d = b, то x = 0, z = 1 – y, если d не равно ни a, ни b, то решений нет;
при a = b = c = d z = 1 – x – y; при a = b = c ≠ d решений нет. е) Если a = b = c = 0, то x, y, z – любые числа; если a = b = c ≠ 0, то z = 3 – x – y; если a + b + c = 0, но не все числа a, b, c равны нулю, то x = y = z; в остальных случаях x = y = z = 1.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь