Задача
Рассмотрим окружность радиуса 1. Опишем около нее и впишем в нее правильные n-угольники. Обозначим их периметры через Pn (для описанного) и pn (для вписанного).
а) Найдите P4, p4, P6 и p6.
б) Докажите, что справедливы следующие рекуррентные соотношения:
P2n =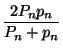 
, p2n = 
(n ≥ 3).
в) Найдите P96 и p96. Докажите неравенства 310/71 < π < 31/7.
Решение
б) Обозначим черезanиbnстороны правильныхn-угольников – вписанного и описанного. CерединыK, L, MсторонAB, BC, CDправильного описанного 2n-угольника являются последовательными вершинами правильного вписанного 2n-угольника. Кроме того, KM– сторона правильного вписанногоn-угольника, точкаEпересечения прямыхABиCD– вершина правильного описанногоn-угольника, аKиM– середины его сторон.
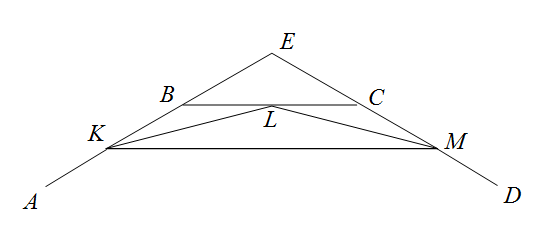
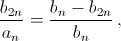то есть 
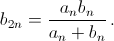Из подобия треугольниковKBLиKLMполучаем 
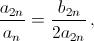то есть 
.
Учитывая, что pn=nan, Pn=nbn, и получаем требуемые соотношения. в) Используя формулы из б) получаем:
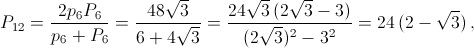
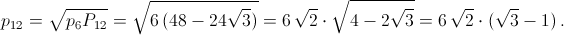
Продолжая, можно дойти до P96 ≈ 6,285429, p96 ≈ 6,282064 и убедиться в том, что 620/71 ≈ 6,281690 < p96 < P96 < 62/7 ≈ 6,285714. Осталось заметить, что
pn < 2π < Pn при любом n.
Ответ
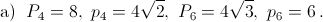
в) P96 ≈ 6,285429, p96 ≈ 6,282064.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь