Многочлен P₁, получаемый по методу Лобачевского, имеет вид  x² – 3x + 1.  Пусть многочлен P_n имеет вид  x² – p_nx + 1.  Тогда многочлен P_n+1 получается подстановкой x вместо x² в многочлен 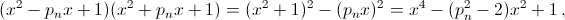    то есть имеет вид  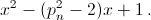   Последовательность {p_n} совпадает с последовательностью {L_2ⁿ}, где L_n – числа Люка (см. задачу 160585). Действительно  p₁ = 3 = L₂  и согласно задаче 164318 рекуррентные формулы для p_n и L_2ⁿ совпадают.

  Согласно задаче 61333 с учётом знаков корней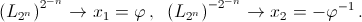  

Ответ задачи отсутствует