Задача
Пусть многочлен P(x) = xn + an–1xn–1 + ... + a1x + a0 имеет корни x1, x2, ..., xn, причем |x1| > |x2| > ... > |xn|. В задаче 160965 был предъявлен способ построения многочлена Q(x) степени n, корнями которого являются числа 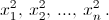 На основе этого рассуждения Лобачевский придумал метод для приближенного поиска корней многочлена P(x). Он заключается в следующем. Строится такая последовательность многочленов P0(x), P1(x), P2(x), ..., что P0(x) = P(x) и многочлен Pk(x) имеет корни
На основе этого рассуждения Лобачевский придумал метод для приближенного поиска корней многочлена P(x). Он заключается в следующем. Строится такая последовательность многочленов P0(x), P1(x), P2(x), ..., что P0(x) = P(x) и многочлен Pk(x) имеет корни
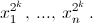 Пусть
Пусть 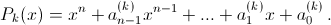 Докажите, что а)
Докажите, что а) 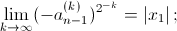 б)
б) 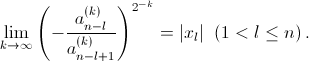
Решение
а) 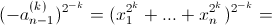
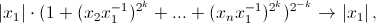 поскольку при k → ∞ выражение в скобках стремится к 1, а показатель степени – к нулю. б) Рассмотрим случай l = 2 (остальные аналогичны).
поскольку при k → ∞ выражение в скобках стремится к 1, а показатель степени – к нулю. б) Рассмотрим случай l = 2 (остальные аналогичны).
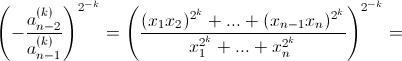
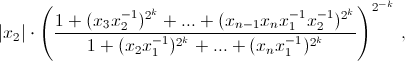
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь