Задача
Решите системы:
a) ![]()
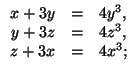
б) ![]()
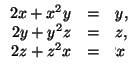
в) ![]()
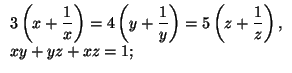
г) 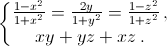
Решение
a) Если одно из неизвестных (например, x) больше 1, то z = 4x³ – 3x = x³ + 3(x³ – x) > 1; аналогично y > 1. Но тогда
x³ + y³ + z³ > x + y + z, что противоречит равенству, получаемому сложением всех уравнений. Значит, каждое из неизвестных не превосходит 1. Так же доказывается, что каждое из них не меньше –1.
Поэтому можно сделать замену x = cos φ. Тогда получаем z = cos 3φ, y = cos 9φ, x = cos 27φ. Итак, cos 27φ = cos φ, то есть
27φ = ± φ + 2kπ, откуда φ = kπ/14 или kπ/13. б) Как легко проверить ни одно из неизвестных не может равняться 1. Поэтому первое уравнение можно записать в виде 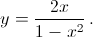 После замены
После замены
x = tg φ получаем y = tg 2φ, z = tg 4φ, x = tg 8φ. Отсюда tg 8φ = tg φ, то есть 8φ = φ + kπ. в) Ясно, что все переменные имеют один знак, поэтому будем считать, что все они положительны.
Положим x = tg α, y = tg β, z = tg γ (0 < α, β, γ < π/2). Тогда tg γ (tg α + tg β) = 1 – tg α tg β, tg γ = ctg (α + β), то есть α + β + γ = π/2.
С другой стороны, 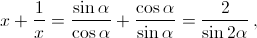 значит,
значит, 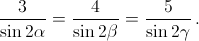 Следовательно, 2α, 2β, 2γ – углы прямоугольного треугольника со сторонами 3, 4, 5.
Следовательно, 2α, 2β, 2γ – углы прямоугольного треугольника со сторонами 3, 4, 5.
Отсюда z = tg π/4 = 1. Найти tg α и tg β можно либо по формулам половинного угла, либо используя свойство биссектрисы: биссектриса угла 2α делит катет длины 3 на отрезки длины 15/9 и 12/9, поэтому tg α = 12/9 : 4 = 1/3; аналогично, tg β = ½. г) Положим x = tg α/2, y = tg β/2, z = tg γ/2 (– π < α, β, γ < π). Тогда два первых уравнения запишутся в виде cos α = sin β = cos γ, а последнее при наших ограничениях, аналогично в), даст условие α + β + γ = ± π. Из равенства cos α = cos γ получаем γ = ±α. Но если γ = – α, то β = ± π, что невозможно.
Итак, γ = α, β = ± π – 2α, sin 2α = sin β = cos α, откуда cos α = 0 или sin α = ½.
В первом случае α = ± π/2, β = 0. Во втором случае α = π/6, β = 2π/3 или α = 5π/6, β = – 2π/3.
Напомним, что 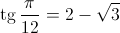 (см. задачу 161169).
(см. задачу 161169).
Ответ
а) (0, 0, 0), ± (1, 1, 1), ± (cosπ/14, – cos5π/14, cos3π/14), ± (cosπ/7, – cos2π/7, cos3π/7), ± (cosπ/13, – cos4π/13, cos3π/13),
± (cos2π/13, – cos5π/13, cos6π/13) и все наборы, получающиеся из указанныхциклическимиперестановками.б) (0, 0, 0), ± (tg π/7, tg 2π/7, – tg 3π/7) и все наборы, получающиеся из указанных циклическими перестановками. в) (± 1/3, ± 1/2, ±1). г) 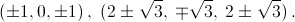
Чтобы оставлять комментарии, войдите или зарегистрируйтесь