Корневые прямые  q = p + 1  и  q = – p – 1  с угловыми коэффициентами ± 1 касаются дискриминантной кривой в точках  (–3, –2)  и  (–3, 2)  (см. задачу 161271). В точках дискриминантной кривой, находящиеся левее этих точек, касательная к ней имеет угловой коэффициент, по модулю больший 1. Легко видеть, что все эти касательные "заметают" область, состоящую из всех точек, находящихся под одной из прямых указанных корневых прямых. Из каждой точки этой области (включая границы) к дискриминантной прямой можно провести хотя бы одну касательную, угловой коэффициент которой по модулю больше 1, что соответствует наличию "плохого" корня уравнения. Таким образом ответом является оставшаяся часть плоскости.

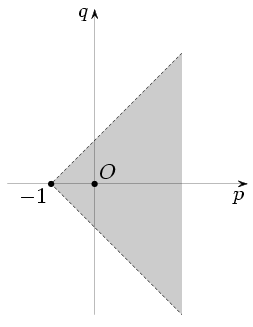
Множество точек, заданное неравенством  p > |q| – 1 (см. рис.).