Задача
Найдите все действительные значения a и b, при которых уравнения x³ + ax² + 18 = 0, x³ + bx + 12 = 0 имеют два общих корня, и определите эти корни.
Решение
Оба общих корня являются корнями трёхчлена (x³ + ax² + 18) – (x³ + bx + 12) = ax² – bx + 6. По теореме Безу оба кубических многочлена делятся на этот трёхчлен: x³ + bx + 12 = (ax²– bx + 6)(cx + d). Сравнивая коэффициенты, получаем: ac = 1, ad – bc = 0, 6c – bd = b, 6d = 12, откуда d = 2, b = 2c, a = c²,
c³ = 1. Итак, a = c = 1, b = d = 2. Осталось найти корни трёхчлена x² – 2x + 6.
Ответ
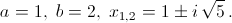
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет