1) Заметим, что 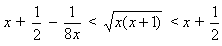   при  x ≥ 1  (оба неравенства проверяются возведением в квадрат).

  2) Пусть  a = ,  b_n = {2^n–1a}.  Тогда b_n – иррациональное число,  b_n+1 = {2b_n}.  В любом из этих случаев  b_n+1 – ab_n < 1 – ^a/₂.

Кроме того, 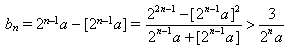    при  n > 1:  2^2n–1 не является квадратом, но кратно 4, а  [2^n–1a]² ≡ 0 или 1 (mod 2),  поэтому числитель не меньше 3.

  3) Пусть  y_n = a^n–1 + a^n–2.  Докажем по индукции, что  x_n = [y_n].

  База.  x₁ = 1 = [a⁰ + a^–1]  по условию,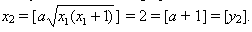  

  Шаг индукции. Предположим,  x_n = [y_n].

  Пусть  n = 2m,  тогда  y_n = 2^m–1a + 2^m–1,  [y_n+1] = 2^m + 2^m–1a,  поэтому  {y_n} = {y_n+1} = b_m,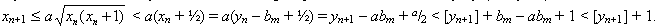 

  С другой стороны, 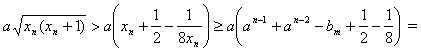  x_n+1 + b_m – ab_m + ^3a/₈ > [y_n+1] – ^b_m/₂ + ^3a/₈ > y_n+1 – ½ + ^3a/₈ > y_n+1.  Следовательно,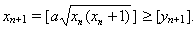  

  Пусть  n = 2m + 1 > 1,  тогда  y_n = 2^m + 2^m–1a,  y_n+1 = 2^ma + 2^m,  поэтому  {y_n} = b_m,  {y_n+1} = {2b_m},

x_n+1 < a(x_n + ½) = y_n+1 – ab_m + ^a/₂ = [y_n+1] + b_m+1 – ab_m + ^a/₂ < [y_n+1] + 1 – ^a/₂ + ^a/₂ = [y_n+1] + 1.

  Если  b_m < ½,  то  b_m+1 = 2b_m, 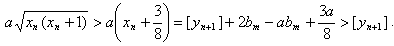   Следовательно,  x_n+1 ≥ [y_n+1]. 

  Если  b_m > ½,  то  b_m+1 = 2b_m – 1.  Кроме того,  ¹/_8xn ≤ ¹/_2^m+3.

  Значит, 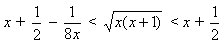  [y_n+1] + ^2–a/₂b_m+1 – ^a/₂ + ^a/₂ – ^a/_8xn ≥ [y_n+1] + ^3(2–a)/_2^m+2 – ^a/_2^m+3 > [y_n+1].   Следовательно,  x_n+1 = [y_n+1].  (Использовано доказанное в 2) неравенство   b_m+1 > ³/_2^m+1a = ^3a/_2^m+2.)

  4) Отсюда следует, что  x_2n+1 – 2x_2n–1 = [2ⁿ + 2^n–1a] – 2[2^n–1 + 2^n–2a] = [2^n–1a] – [2^n–2a],  а это и есть (n–1)-й знак после запятой в двоичной записи числа a.

Ответ задачи отсутствует